| Wyvern Semiconductors | Expert in Digital IP Solutions |
|
Data Compression Implementationby Simon Southwell10th September 2004
1 IntroductionIn this article, as a working example, we'll look at implementing a simple LZW algorithm (slzw). In doing this we can highlight the limitations and boundaries that exist when turning an algorithm into a working implementation. LZW is chosen as it follows naturally on from the previous article, and because it forms the basis of many practical implementations, including GIF graphics files, hardware compression in tape drives and many other applications. In section 3 of the previous article the LZW algorithm was discussed in general terms and idealistically. In order to realise a practical implementation, whether hardware or software, some boundaries must be defined and choices made. In the next few sections a simple software implementation is described, laying out where choices are made, and what alternatives might exist, as well as alluding to the architecture of a hardware solution. It may seem that the discussion is ordered the 'wrong' way round, in that we'll look at the actual compression and decompression code last, but this is because those functions are built on the features of the ancilliary functions. The compressor matches and builds entries in the dictionary and sends on codewords to the packer. The decompressr gets codewords from the unpacker and reads and builds entries in the dictionary. So we need to understand these functions first. So let's look at the dictionary. 2 DictionaryIn the LZW discussion of the previous article, there was an unspoken assumption that is actually impractical—the dictionary is infinitely large. In this section we are going to look at some bounding of the dictionary to make it practical, and how a dictionary is realistically implemented. The goals are twofold. Firstly, what sensible limit on dictionary size is acceptable, and secondly, how can we construct it so that it is reasonably fast to use. 2.1 Bounding the DictionaryThe actual size (in bytes) of a dictionary is determined by two things: the size of each entry, and the number of entries. Let's bound the latter of these first (why not!). Making the dictionary as large as possible more nearly approximates the ideal of infinite, but you'll need much more space to store it, and (perhaps) a very long time to search it for an entry. Making it very small (and it must have at least 256 + 1 entries, or we're not making a compressor!) is not likely to yield a useful implementation. A sensible approach is to choose a power of 2 size from 2^9 upwards. Each increment yields a dictionary which is double in size, and requires double the resources, so this quickly becomes a limiting factor. In all practical LZW based implementations I have seen (both software and hardware) dictionaries are between 1K and 64K bytes. Any smaller and compression figures are severely hit; any larger, and the gain in performance is negated by the resources required. So we will choose a midway point of 4K, which is used in the DCLZ algorithm embedded in DAT tape drives. By making this choice, we have significantly bounded the dictionary. It has 4096 entries, and this limits the maximum codeword width to 12 bits. Knowing this defines the entry width to 12 + 8 = 20 bits, as the dictionary entry pointers are the same size as the codewords (indeed they are synonymous). As a minimum then, we need (4096 x 20)/8 = 10K bytes of resource for a dictionary. 2.2 Resetting ChoicesNow we've bound our dictionary, there is the problem of what to do when it's full. This question opens up a whole can of worms, as there many possible choices, which may have some advantages for some cases, whilst being quite disadvantageous in others. The issue is, when the dictionary is full, how relevant is it to current input data? If the data remains similar in character (say we're compressing a large source of English text), then it may be very relevant. On the other hand, if we're compressing, say, an archive file which contains an eclectic mix of small files of different types, then the dictionary will become irrelevant when the file type switches after it's become full. The simplest thing to do is reset the dictionary when its full (or at least when we want to build a new entry after its full). This is great, but there is a penalty in that compression ratios suffer after a reset when there are less entries to match against. An advantage is that the compression and decompression resets don't have to be explicitly synchronised, since the dictionary is built up in the same manner in both cases, and reaches full in the same place (well, almost—see below). A more elaborate method is to somehow measure the 'effectiveness' of the dictionary, and only reset it when it becomes 'ineffective'. How to do this is the subject of much research and patent filing, and without going in to details, measuring the compression ratio over a set number of input bytes can achieve this. An even more complex enhancement is to only reset some of the entries which are less 'relevant'. But that is beyond the scope of this article. Suffice it to say that the common factor with these methods is that the resetting of the dictionary is done externally to it. Therefore we need to synchronise between compression resets and decompression resets. This is usually done by inserting a marker in the compression stream. Reserving one of the codewords used for a dictionary entry is one method. In DCLZ this is the Reset codeword (value 0x001). Whenever the dictionary is reset, the compressor inserts a Reset codeword. On decompression, if a Reset is encountered then the dictionary is reset before continuing. The advantage of the special codeword is that decompression is immune to the method used to determine reset on compression. So it can be made completely configurable, dynamic, or whatever, during compression without precluding the decompressor from decoding the data—even a different implementation by a third party. Having said all that, we're going straight back to square one, and choosing to implement a 'reset on full' approach. 2.3 Implementing a DictionaryWe may have defined a dictionary's boundaries, but this doesn't tell us how to use it. There are two main things we must be able to do with the dictionary; add new entries and determine whether a given value is in the dictionary (is 'matched'). Building an entry is a trifle more involved than simply writing a value (but not much more!). The address used when writing the entry is managed by the dictionary itself. An incrementing counter is kept, initially set to the lowest dynamic entry, and incremented as each new entry is written. This counter is managed by the dictionary, but is going to be needed externally and so must be exported (preferably behind a 'data hiding function', but our example won't go this far for the sake of clarity). An example function is shown:
static unsigned int build_entry(codeword_type codeword, byte_type byte, boolean compress_mode) { static unsigned int codeword_len = MINCWLEN;
if (next_available_codeword == DICTFULL) { next_available_codeword = FIRSTCW; codeword_len = MINCWLEN; return codeword_len; }
dictionary[next_available_codeword].pointer = codeword; dictionary[next_available_codeword].byte = byte;
if (compress_mode) indirection_table[codeword][byte] = next_available_codeword;
if (codeword_len < MAXCWLEN) { if (next_available_codeword == (1U << codeword_len) - (!compress_mode ? 1U : 0U)) codeword_len++; } else if (!compress_mode && next_available_codeword == (DICTFULL-1)) codeword_len = MINCWLEN;
++next_available_codeword;
return codeword_len; }
This code assumes a pre-existing global array (dictionary) each entry of which is a structure with a pointer and byte field. A codeword and byte to be written is passed in, and a flag to indicate whether we're compressing (as opposed to decompressing—the dictionary routines are common to both). The first lines test for a full dictionary and reset it if it is, before returning. The entry to build in that case is effectively discarded. If the dictionary isn't full the codeword and byte values are written to the dictionary at the address indicated by the next_available_codeword counter, which is incremented before returning. Before returning, though, some additional processing is done. An indirection table is updated. More on this below, but it is only a method of quickly locating an entry during a match search, which could be done in many different ways, such as a hash table or even a linear search if speed is not important. The next bit of code is determining whether the current dictionary entry (next_available_codeword) is larger than the current packing/unpacking width (see section 3 below). If it is, codeword_len is incremented to increase the packing/unpacking width. Finally, when decompressing, the entries being built lag behind compression by one codeword (the famous KωK exception case is caused by this), so we have to reset the codeword_len one entry early to compensate. Searching the dictionary to see whether a given data value matches one already built is more difficult. As mentioned above, one solution is to linearly search from the first dictionary entry to the last built entry, but this is very slow. A hash table is a much better idea. For those unfamiliar with this technique, basically instead of storing the entry linearly against an address, an address is generated from the data, trying to make it pseudo-random like. So usually, bits are jumbled up, and/or inverted etc. At this data dependant location is stored the 'codeword' (next_available_codeword) that would have been the address of the linear implementation, along with the data itself (or some unique part of it). When searching for an entry, the hashed address can be regenerated using the same algorithm, and that entry inspected for the data we're try to match. If it's the same, then the stored codeword is retrieved. This sounds great, and is very fast, but has some drawbacks. For an effective hashing algorithm, the number of entries must be greater than for a linear dictionary. This is because of another drawback, different values can generate the same address (whatever hashing algorithm you come up with). This is alleviated somewhat by making the hashing dictionary bigger (at the cost of additional resources) and making 'collisions' less likely, but even so, these collisions must be dealt with, and extra complexity is added to detect a collision and end up at a unique location for a given entry. This method can be used, however, in both software and hardware implementations affectively, and some early DCLZ hardware in DAT tape drives used this method. More recently, as of writing, hardware implementations use a type of memory called content-addressable-memory (CAM). CAMs can act like ordinary SRAM, but in addition allow a parallel search of a value in all its locations at once, returning a 'match' status and an address of the matched data (if any). We can't do this same technique in software, but we can avoid the hasing penalties at the expense of more memory requirements—but it is much more plentiful on a computer than on a silcon chip anyway. The technique makes use of an indirection table, which is nothing new, but its use with respect to an LZW based dictionary is novel to me as far as I know. We can take advantage of the fact that each entry in the dictionary is unique (if the dictionary is a valid one!), and that it is contiguous from the first entry to the top; i.e. has a valid entry, without holes, up to next_available_codeword. The table is a two dimensional array which is 256 wide by 'dictionary size' long (4K in our case). It could have been simply a linear 256*4K array, but the important point is that there is an entry for every single codeword/byte pair that can exist. When a new entry is built in the dictionary, the address of the new entry is stored in the indirection table at indirection_table[codeword][byte]; i.e. the unique location defined by the data. This is what's happening in the build_entry() function above. When we want to match a particular value (a codeword and byte pair) in the dictionary, the dictionary address is fetched from the indirection table and the dictionary entry compared with the match data. If it is the same then we have a match, and the address from the table is the codeoword we need, or we haven't matched, and the data is not in the dictionary. Let's look at the code:
static codeword_type entry_match(codeword_type pointer, byte_type byte) { codeword_type addr;
addr = indirection_table[pointer][byte]; if (addr < FIRSTCW || addr >= next_available_codeword) return NOMATCH;
if ((dictionary[addr].byte == byte) && (dictionary[addr].pointer == pointer)) return addr;
return NOMATCH; }
Hopefully it is clear that the above code implements the described operation. The only extra bit is a check that the retrieved address is within the valid dictionary range, and returing a NOMATCH if it isn't. By doing this we avoid having to initialise the table (which can be quite large), and random invalid values cause a mismatch. Of course a random value may lie within a valid dictionary location, but this still doesn't matter. If the codeword/byte pair has never been written in the dictionary, then that random value can't contain the value, since all dictionary entries are unique, and we mismatch. If the value has been written in the dictionary, then the indirection table won't have a random value in it at that location, and we get a match. These two functions constitute the two operations needed by the compression and decompression code and, as stated before, the next_available_codeword counter, defining the top of the valid dictionary, is exported (in our case a simple global) to enable inspection of the reset state. One last operation is needed from the dictionary, and that is to read a particular location in decompression, where incoming codewords define this address. In the example code this is acheived by making the dictionary global and reading it directly. Again this is purely for clarity—keeping the number of lines of code to a minimum is essential in a document, but ideally the dictionary would have a data hiding function which returned the pointer and byte value of a given entry, leaving the dictionary array completely local to the dictionary routines. So we have a dictionary. Before moving on to compression and decompression we still need some more functions. To get the most performance from our implementation, the steady stream of codewords need to be 'packed' as tightly as possible, and subsequently 'unpacked' before decompressing. We'll look at this in the next section. 3 Packing and UnpackingThe pure LZW algorithm discussed in the previous article will generate a stream of codewords. By bounding the size of the dictionary (e.g. to 4K bytes) that stream of codewords will be fixed (to 12 bits for a 4K dictionary). Since the codewords might not exactly fit into bytes, it is useful to 'pack' the codewords so as to avoid wasted padding bits to make the codewords align to byte boundaries. Packing simply means appending the next codeword at the bit position after where the current output codeword finishes. Unpacking is simply the reverse. Since the codeword size is known, enough bytes are read to have a whole codeword, which can then be passed into the decompression processing. Any remaining bits are held over and used as the begining of the next codeword. 3.1 Dynamic PackingThe above scheme is all very well, and it avoids the insertion of redundant bits (not good in a compression algorithm). However, from the previous article, you may have noticed that initially, when only a few dictionary entries have been built, all the codeword values are small. As the dictionary is filled, higher value codewords become possible. So, when packing, we can take advantage of this and pack the codewords more compactly by treating them as being less wide as the maximum width. For example, for a 4K dictionary with 12 bit codewords, initially 9 bits are all that are required to pack until the dictionary has an entry in 0x200 (512) when 10 bits are needed, and so on until entry number 0x800 (2048) is built, when 12 bits (the maximum) are needed. There's a choice about whether to pack at the new width when the entry is built, or when a wider codeword must be packed (since there may be a delay between the two). We'll discuss this later, but suffice it to say that we can inform the packer what the current width requred is, and adjust the packing accordingly. This gives us the best packing of codewords we can acheive. One other arbitrary choice we have is whether to pack codewords least- or most-significant byte first. It doesn't matter which, but we have to choose the same between packing and unpacking! I prefer least significant first, and this is used in a format called DCLZ. But another algorithm ALDC uses most-significant. Using lsb, let's have an example. Suppose we're packing 9 bit codewords: 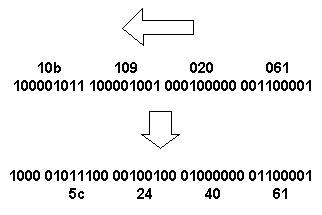
In the above sequence, time is flowing from right to left, so that the codeword sequence (in hex) is 061, 020, 109, 10b, with the binary values underneath. Hopefully you can see that the second row of binary values are the same bit sequence as the first, but have been split at every eighth bit instead of ninth. Converting back to hexadecimal values now gives a byte sequence of 61, 40, 24, 5c. We have 4 bits left over, which will form part of the next byte, or if this is the last byte, would be flushed to a byte boundary to give 08. Unpacking is the reverse, with the bytes read and the correct number of bits for a whole codeword pulled off to form a stream of unpacked codewords. Now to determine when to update the packing width. The simplest approach is to set the width to match the last built dictionary. Since we can only output codewords that are built in the dictionary, we'll never find ourselves in the position of trying to pack, say, a 12 bit codeword when we're only packing at 11 bits. It is also easy to synchronise between packing and unpacking as the dictionary is built in the same manner between compression and decompression. There are two issues with this however; a small and a not so small one. The small issue is that the packing/unpacking has to have access to some internal dictionary state; i.e. the highest built entry. Not a disaster, but it would be better if these mostly disassociated functions remained decoupled. The second more relevent issue is that when an entry is built at one of the bit boundaries, it cannot be used straight away. At least one (necessarily smaller) codeword will be output first, and more likely several codewords. These codewords will be packed more loosely than is strictly necessary, wasting bits. We can solve this by waiting to up the packing width until a codeword is ready to be output that requires the wider width. The packer can determine this by inspecting the upper bits of the codewords and if any are set higher than the current packing width, it can increase as necessary. There is also no need to inspect any dictionary state, and its input is all that's required. Unfortunately, during unpacking it is not possible to know in advance when the packer would have increased the width. So some sort of indicator must be inserted into the data stream to inform the unpacker to increases its width. This is usually done by reserving one of the dictionary codewords to have a special meaning. It makes sense if we choose one of the lowest numbered codewords (e.g. 0x100) as this will be nine bits, and so most efficient. In DCLZ, this codeword is called a 'Grow' codeword, and (for strange historical reasons I won't go into) has a value 0x002. Whenever the packer receives a codeword which is too big, it inserts a Grow codeword (at the current packing width) and increments its current width. When the unpacker receives a Grow codeword, it increments its current width, and then discards the codeword as the decompressor knows nothing of this type of command. It should be noted that it is possible to jump more than one width (from say 10 to 12), and the packer must insert as many Grow codewords as necessary to get to the required width. The advantage of this method is that it decouples the dictionary from packing and doesn't waste bits in the packed codewords. However, bits are wasted in outputing a Grow codeword, and a dictionary entry has been wasted to reserve a number for the Grow. In addition it is more complex to implement and the benefit may be dubious. Although there may be a significant lag between a dictionary entry being built and its codeword being output, usually this is not the case as much repetition is localised in common data (though there are no hard and fast rules on this). My own feeling is that it is an optimisation too far, and that dictionary synchronised packing width is simpler and of no significant degradation in performance. One final thing before we look at some code implementation. If the dictionary ever gets reset, the packing/unpacking width must also revert to its minimum value. This may mean that the packer/unpacker must interpret another special codeword (Reset), or have further tendrils into the dictionary to determine when its is reset. 3.2 ImplementationLet's see some code for a packer: static void pack(codeword_type ip_codeword, unsigned int codelen, boolean flush, FILE *ofp) { static unsigned long barrel = 0; static int residue = 0;
barrel |= ((ip_codeword & CODEWORDMASK) << residue); residue += codelen;
while (residue >= (flush ? BITSIZE : BYTESIZE)) { putc((barrel & BYTEMASK), ofp); barrel >>= BYTESIZE; residue -= BYTESIZE; } } This function has four inputs. The codewords arrive as ip_codeword, and the packing width has been determined from dictionary externally, and is input as codelen. The flush flag indicates the end of data case mentioned in the above example, where the final bits must be padded to a byte boundary. Finally *ofp is simply a file pointer to the destination output stream. The code works by appending the ip_codeword onto barrel (a barrel shifter) above any bits that remain on the shifter, as indicated by residue. For every ip_codeword added, residue is incremented by the current width (codelen). Then, for as many whole bytes as there are on the barrel shifter (as indicated by residue), the bottom eight bits are output to the output file, the barrel shifted right 8 bits and residue decremented by 8. The exception to this is if flush is set, when bytes are output until there are no residue bits (residue is 0). An important point to note is that the maximum number of bits on the barrel shifter is never more than 7 plus the maximum codeword width (e.g. 19 for a 4K dictionary). So the type of the barrel in C program (or width of a register vector in a hardware implementation) needs to take this into consideration. Unpacking is the reverse of packing.
static int unpack(codeword_type *codeword, unsigned int codelen, FILE *ifp) { static unsigned int residue = 0, barrel = 0; short int ipbyte;
while (residue < codelen) { if ((ipbyte = getc(ifp)) == EOF) return EOF; barrel |= (ipbyte & BYTEMASK) << residue; residue += BYTESIZE; }
*codeword = (barrel & ((1 << codelen) - 1)); residue -= codelen; barrel >>= codelen;
return ipbyte; }
The arguments are similar to pack(), but *codeword is a pointer where unpack() will output a codeword. The codelen input is the same, and *ifp is the input stream file pointer. So here, the unpacker appends bytes to the barrel shifter, adding 8 to residue, until enough bits for a codeword are read. The bottom codelen bits are then returned in *codeword, the barrel shifted right to delete those bits, and residue adjusted accordingly. One special case is when end-of-file is reached (EOF). Here no processing is done, but EOF is returned to tell the decompressor that no more data is coming. So, normally we must return something other than EOF, which what the last line is about. So now, with a dictionary and packer/unpacker, we have enough to look at compression and decompression (at last!). This is discussed in the next section. 4 CompressionHaving (wisely) defined the dictionary and packing functions, compression becomes a breeze. We simply keep pulling bytes in, matching the byte and the previously matched codeword (if any) in the dictionary until there is no match. Then we output the most recent matched codeword and build a new entry for this codeword and byte that we mismatched. The code is shown below:
static void compress(FILE *ifp, FILE *ofp) { codeword_type previous_codeword = NULLCW; unsigned int code_size = MINCWLEN;
codeword_type match_addr; int ipbyte;
while ((ipbyte = getc(ifp)) != EOF) if (previous_codeword == NULLCW) previous_codeword = ipbyte; else if ((match_addr = entry_match(previous_codeword, ipbyte)) == NOMATCH) { pack(previous_codeword, code_size, FALSE, ofp); code_size = build_entry(previous_codeword, ipbyte, TRUE); previous_codeword = ipbyte; } else previous_codeword = match_addr;
pack(previous_codeword, code_size, TRUE, ofp); }
So, the compress() function has two arguments, which are the input and output file pointers. The heart of the function is the while loop pulling in bytes into ipbyte, until the end-of-file. The special case of the very first byte is caught when previous_codeword is NULL. The previous_codeword variable holds the best match we have so far, but at the beginning we haven't done a match. So in this case the ipbyte value is simply copied to previous_codeword, as we now have an implied match on the 'root' codeword for the input byte. In our scheme root codewords run from 0 to 255 matching the bytes—a sensible choice I trust you'll agree. However, not all schemes follow this obvious choice and DCLZ, for example, has root codewords which run from 8 to 263! (It has 8 reserved codewords from 0 to 7). Normally, we pull a byte in and do a match by calling the dictionary function entry_match(). If we have a match, then the returned match address becomes the previous_codeword, and we go round the loop again. If we didn't match, then the best match we had so far is output by sending to the packer (see section 3) and a new entry built for the failing match. We have output previous_codeword, but the byte in ipbyte is not yet represented in the output, so we must copy it to previous_codeword as it is now our best match (or its root codeword value is, which is the same thing for us). When end-of-file is reached, and we drop out of the loop, the output packer is called once more, as we will have a best match still in previous_codeword, even if it is just the last byte's root codeword. The pack() function is normally called with its third argument as FALSE, but the last call has it set to TRUE. This informs the packer that no more data is coming and to 'flush' to a byte boundary. Also the code_size variable defines the 'packing width' to use. It is based on the highest dictionary entry built, and is set when build_entry() is called which returns the decoded value. 5 DecompressionDecompression is only slightly more involved than compression. Here we pull in a stream of codewords, and traverse the dictionary stuffing the byte values of the entries onto a stack. When a root codeword is reached, the stack is flushed to the output, reversing the order of the bytes read from the dictionary. Let's look at some code: static void decompress(FILE *ifp, FILE *ofp) { static byte_type stack[MAXDICTSIZE]; static unsigned int stack_pointer = 0;
codeword_type ip_codeword, prev_codeword = NULLCW; unsigned int code_size = MINCWLEN; byte_type byte; codeword_type pointer;
while (unpack(&ip_codeword, code_size, ifp) != EOF) { if (ip_codeword <= next_available_codeword) { pointer = ip_codeword; while (pointer != NULLCW) { if (pointer >= FIRSTCW) { if (pointer == next_available_codeword && (prev_codeword != NULLCW)) pointer = prev_codeword; else { byte = dictionary[pointer].byte; pointer = dictionary[pointer].pointer; } } else { byte = pointer; pointer = NULLCW; } stack[stack_pointer++] = byte; }
while (stack_pointer != 0) putc(stack[--stack_pointer], ofp);
if (prev_codeword != NULLCW) code_size = build_entry(prev_codeword, byte, FALSE); prev_codeword = ip_codeword; } else { fprintf(stderr, "***decompress: Error --- UNKNOWN CODEWORD (0x%03x)\n", ip_codeword); exit(DECOMPRESSION_ERROR); } } }
Like compression, a 'while' loop forms the heart of the function. Codewords are fetched by calling the unpacker (unpack()) which returns a codeword into ip_codeword. A check that the codeword is valid is done before proceeding (it can happen!) and an error printed if something's wrong. Otherwise we traverse the dictionary, which is what the inner 'while' loop is doing. When pointer (which holds the current dictionary address whilst we're traversing) is a root codeword (less than FIRSTCW) then we construct a root entry, making the byte value simply the pointer (in our example) and setting prev_codeword to NULL. If it's a dynamic codeword then we get the new byte and pointer value directly from the dictionary. However, we have to detect and deal with the KωK case. This is detected when the pointer is equal to the dictionary's next_available_codeword value (and this is not the first time through the loop—prev_codeword is not NULL). In that case we reconstruct the pointer from the prev_codeword of the last time round the loop, and the byte value is also correct from last time (i.e. the last output byte that terminated the previous string). In all cases, the byte value we determined gets added to the stack. When we reached a root codeword, the inner loop terminates and the stack gets flushed to the output, reversing the bytes. A new entry in the dictionary is then built (except first time round) using the prev_codeword value and the last byte pushed on the stack. The input codeword we just processed then becomes the previous codeword for the next loop. As in the packer during compression, the unpacker is informed of the current codeword width based on the dictionary's highest entry, and code_size is updated on every call to the dictionary routine build_entry(). 6 ConclusionsSo that's pretty much all the code we need. A top level main() function can define the input and output streams (*ifp and *ofp) and select between compression and decompression. Actually I have done this for you and the entire code can be accessed on github by clicking here. This is a single, self contained file (slzw.c) which should compile on just about any platform (I've tried Solaris, Linux and Windows—you'll need getopt() for windows; try here), and has all the functions already mentioned and everything else that's required. The whole thing is less than 250 lines of code, and still achieves a satisfactory performance in both speed and compression ratio. Feel free to try enhancing the code for larger dictionaries, different reset strategies, or any other enhancement you can think of. The code is copyright free (though this text isn't) and the patent for the LZW algorithm, held by Unisys, has recently expired in all countries. So you are also free to incorporate this code into your own products without violating the law. 7 Downloadable Code and Useful Data Compression LinksMore detail on lossless compression and real implementations of data compression can be found via the following links.
Last updated 10th March 2017 © 2004-2017 Simon Southwell. All rights reserved. simon@anita-simulators.org.uk |
