| Wyvern Semiconductors | Expert in Digital IP Solutions |
|
Notes on Data Compression & Related topicsby Simon Southwell29th March 1999
1 Introduction1.1 InformationWhen we receive junk mail through the door, we can often feel that it contains almost no information, and the bin is the only fit place for it---often unopened. But this feeling of 'content free' communication is really a subjective assessment. For a definition of information that will be useful for us, we need to remove our 'human' interest. Carrying on the junk mail analogy, if, every month, you receive a letter from a credit card company, extolling the virtues of their particular credit card, perhaps because it has a picture of a Moose on the front, then the information content of letters AFTER the first letter was sent are, indeed, information free. When you receive the letter you know exactly what it contains, and it can go straight in the bin. Perhaps, though, the credit card company are becoming more desperate each month to win your business, and are reducing the first year's APR each time the send you the letter. The rest of the bumph is the same, but the APR value is different each time. So, the credit card company could just send a postcard with a number on it---the new APR being offered. Therefore the information content is not zero, but you should be able to see that it is still small. Now suppose, on another day, another credit card company sends you a letter, but they have come up with a scheme where by the more you borrow, the more they pay you interest. In addition they give away charitable donations to save Moose from the illegal Moose slave market every time you use their card. Now, you must agree, you are not likely to expect such a communication. If one turned up, you'd probably not believe a word, but you would not have expected it. Therefore its information content is very high. None of what is in the communication was known to you before, and now you know. This, then, gives us a definition of information content: information content is proportional to the data's 'unexpectedness'. Relating this to computer signaling, suppose we are receiving a serial bit stream, 1's and 0's at regular intervals. Now suppose we always receive a steady stream of, say, 1's. Initially the information content is high, the first bit could be either a 1 or a 0. However, as time passes, and 1s continue to arrive, the amount of information the signal is conveying heads towards zero, as the subsequent values become increasingly predictable. At the other extreme, suppose the bit stream indicates the flip of a coin, with one bit for each flip; 1 for heads, say, and 0 for tails. Assuming the flipping is not biased in any way, we cannot predict the value of the next bit to be received by looking at the present, or any of the past bits. The incoming signal is totally random, and contains 100% information. However, suppose that someone at the transmitting end forgot to connect up the transmission wire to the transmission electronics, and instead of coin flips, the line is floating around randomly, so that a random sequence of 1s and 0s is received at the other end. What is the information content of the received signal now? It's 100%! The signal at the receiver is still totally unpredictable. Just because some person is attaching meaning to the signal (i.e. the result of coins being flipped) doesn't change the information value, even when the data doesn't actually have a intended meaning. Indeed, one can argue that the signal in the example is conveying information about the voltage that the loose transmission wire is at, and some thing about the detection circuit's characteristics for distinguishing 1s and 0s. Meaning is only some that we add to information. Somewhere between these two extremes, totally predictable and totally random, lies all the values in between. Much data that we produce contains much information, but it isn't totally random. Take English text for example. Suppose one is reading English text, one character at a time (I don't recommend this). If one comes across a 'Q' (or a 'q'!), I'd bet you would be almost certain that the next character would be a 'u' (but less likely 'U'). You then find you are reading a memo regarding Australia's leading airline and it turns out to be an 'A'. If the next letter turned out to be 'X' then you might feel a typing error had occurred. So we see that we're in this grey area where we can give a good guess of what might follow based on what we have already seen. It's not 100% as we've seen, but the data is not random either. Much data is like this; the data contains information, but is not 100% efficiently encoded, and redundant, predictable, data is contained within it. It is this characteristic of some data that allows us to 'compress' the data. What we need to do is encode the data more efficiently such that every bit contains information. 1.2 Compression ApplicationsThe need for more and more secondary storage has been apparent in recent years due to the growth in the area of information technology. Transfer of data over transmission media has also increased, putting large demands on bandwidth. Solving some of these problems has led to technological advances and innovation, such as fibre optics, read/write optical disks and helical scan tape drives. All these advances have increased bandwidth and storage capacities, but often have only just satisfied the ever increasing demands. One solution for an 'instant' increase in capacity of a medium is to compress the data, using an encoding scheme which represents this data in fewer symbols than the original data set. This will be possible if the data is structured 'inefficiently' and contains redundancy, as discussed earlier. Compression methods have been around for a while, but only in more recent years, with the maturing of VLSI technology, has it been possible to make practical compression implementations at high enough rates to used in useful applications. Compression methods may be implemented on Digital Signal Processors (DSPs), or, for the maximum data rates, in dedicated hardware, as ASICs (Application Specific Integrated Circuits). There are two major classes of data compression techniques:
Lossy algorithms act on data which has redundancy in information which is 'not critical' in order for the data to retain 'meaning'. This usually means data that is to be interpreted by human perception. The most classic cases of this type of data are images (either still or moving pictures) and audio (either voice or music). Of the former type, an example is the JPEG (Joint Photographic Expert Group) standard. This takes advantage of the fact that high frequency components in an image are much less important (for human interpretation) than low frequency components, and it thus reduces (or loses) some of the information in this part of the data content in order to compress the image into a smaller space. Lossy algorithms are also characterised by achieving high data compression figures, as one might expect if data can be thrown away. But this all depends on just how much data can tolerably be lost. After all, in the limit, continued compression will result in just a single bit, but this carries no interpretable data whatsoever. By cutting down this data to smaller sizes, reduced storage requirements are not the only benefit. A fair sized image may be 2MBytes when raw data, but might compress down to 50KBytes. Imagine downloading this image over the web at, say, 5KBytes/S (on a good day). The original image would take nearly three and a half minutes. Compressed, however, and the image is transferred in twenty seconds. Lossless algorithms, by contrast, do not 'lose' one single bit of data, and any compressed file is decodable to its original form. Here the algorithms work on data redundancy due to 'inefficient' representation---effectively, on average, more than 1 bit is used to store 1 bit of information . If the data is 100% efficient, then no lossless data compression technique can compress this any further, and will in fact expand the data slightly due to its own coding overheads. However, much data does have this type of redundancy in it; databases with largely empty search table, source code with repeated spaces and frequent key word strings, English text and so on. In the world of computer storage compression of data is desirable for two reasons. Firstly, more data can be stored per unit of media (reducing the cost of that media) and secondly the transfer rate to the device is increased in proportion to the compression rate (with a sufficiently fast compression device, and a large enough buffer), thus reducing the storage time for a given unit of data. It, of course, goes without saying that lossless compression techniques are used exclusively in computer secondary storage, where all types of data are to be stored, and these types are not predictable in advance. Thus 'universal' compression algorithms are utilised. It is possible that data is compressed by the computer system itself before sending to secondary storage, but this is most likely to be much slower than the transfer rate achievable between the host and a storage device. Dedicated hardware could reside on the host to speed this operation up considerably, but this may become a resource with multiple demands on it from several data transfers that may be required at any one time, causing a bottleneck. The fastest solution of all is to have each storage device contain within it its own dedicated compression hardware, to compress data on-the-fly as it arrives at the device, and to decompress it as it leaves. The host is not involved and only 'sees' an increase in the storage capacity, and an increase in the maximum sustainable data transfer rate. So, which algorithm to choose? Which is the best? There are certainly a few to choose from (refs here), and, as with many engineering problems, there are trade-offs to be made before a final implementation is decided upon. These problems can be as diverse as the maximum amount of dedicated memory that's required or who owns a particular patent and dictates the licencing agreements for that patent. In the following sections we will look at some lossless algorithms in a general manner, followed by a more detailed look at how two of these algorithms may be turned into algorithms that can (and are) used in embedded hardware compression 'engines' in data storage devices. 2 Lossless Data Compression TechniquesLossless compression algorithms (sometimes referred to as noiseless or reversible algorithms) are characterised by the ability to retrieve the pre-encoded data with 100% accuracy. They all attempt to re-encode data in order to remove redundancy, and this implies that data with no redundancy cannot be compressed by these (or any other) techniques without some loss of information. Indeed all these algorithms will have some degree of overhead in their encoding methods and will therefore actually expand non-redundant data. An example of such data might be a data set that has already been compressed. Lossless data compression techniques do not always remove redundancy with 100% efficiency, and often algorithms with different emphasis are used together to give more efficient compression. Or perhaps some pre-processing of data (which doesn't compress) is used in order to make the compression more favourable for the compression technique. E.g. the Barrow-Wheeler transform (BWT). Many algorithms exist with broadly similar characteristics, and sub-variants of these abound in countless measure, each trying to squeeze out the last drop of efficiency. In the following discussions, various different types of algorithm are given a perusal in order to make comparisons, and to give a context to two particular schemes, which we will look at most fully. As had been stated before, one may implement data compression as software running on a CPU, and much has been written on software implementation (see Nelson and Gailly 1996 for an excellent account). To give a different flavour, I want to look at these techniques with an hardware implementation bent. Hopefully this will give a different perspective on the subject, but it will also place different constraints on us that might not be applicable to a software implementation. For example, we are likely to want to compress data in excess of 40Mbytes/s, but the amount of memory available to might be less than 1Kbyte. So what gives! Well, we will have to design an ASIC or FPGA, no small task, and we are likely to fall short in compression ratio compared with a good software compression program; but a Formula 1 racing car might not be comfortable, but it sure leaves a fat Mercedes standing. So let's actually look at our first strategy-run-length encoding. 2.1 Run Length EncodingThis is probably the simplest algorithm to understand, though it is quite powerful for particular types of data that have certain characteristics, as we shall see. This algorithm works by substituting a run of repeated characters with a single instance of the repeated character followed by a count indicating the repetition number. So, for example, suppose we had a data set consisting of the following sequence of characters from a 3 character alphabet:
AAAABBBBBBBCCCCCCCAAACCCCCCAAAAAAA This might be encoded as:
A4B7C7A3C6A7
The new encoding has added some extra 'symbols' for encoding the run length, but in
this very simple scheme we have compressed the character sequence by 34/12 = 2.8.
Of course, the scheme shown is too simple to be practical (you could make it more
efficient, for instance, by avoiding having to encode single characters as ' Even in a practical scheme, you should be able to see that it will only be good if the data is compresses has a high instance of repetition. This characteristic is not shared universally between data sets, and run length encoding is often restricted to data which are essentially bit streams (hence have a two character alphabet, 1 and 0) and which also has a high likelihood of repetition, such as one might find in graphical data; e.g. bitmaps. It is also sometimes used as a post processing algorithm of other compression techniques where their output has some of the favourable characteristics of run length encoding. 2.2 Huffman EncodingThis scheme (Huffman 1952) is a 'variable-length' encoding. It is still widely used today, but can be quite complicated to implement. The general aim is to have a set of uniquely identifiable 'codewords,' which have different lengths, and then assign the smallest codewords to represent the most frequent characters in the data set. Of course, identifying which characters (or more generally, symbols) occur most frequently is not an easy task. We will need a 'model' of this character frequency; i.e. a table of probabilities for the occurence of any given character. There are many ways to do this, but the simplest to understand is where the entire data set is processed, counting character occurences as we go. The table is then constructed as 'number of characters X divided by total number of characters in data set.' Actually, for the method we're about to describe, the character totals are all we need, as only their relative rank is important and we want to avoid any non-integer arithmetic in an implementation. So, we can easily rank each character in terms of its frequency for a given data set. Now we need a coding scheme with the following attributes. It is made up of a variable length set of codes, and each code is uniquely identifiable from all the others. It isn't necessarily obvious how we might do this. One can't simply assign low numbered codes with less bits, as in 0, 1, 10, 11, 100 etc. Given a bit stream of, say, 010101001101010 the coding scheme could yield many different interpretations. The way to proceed is to have a coding scheme whereby no code is a prefix of another code. For example: 00, 10, 11, 010, 011 etc. Here, two bit codes are 00, 10 or 11. This leaves 01 as an unused two bit number. All other codes must use this sequence as the first two bits of their code. By expanding a scheme like this for a more practical number of codewords (such as 256) an implementation can be realised. Note, however, that it is not possible to have a code of a maximum N bits encode 2N codewords, and the longer codewords will 'expand' the characters they encode. Some characters must be more frequently encountered than others. An algorithm can be described which automatically sort the codes for each character, assigning the smallest codes to the most frequent characters. The algorithm is going to build a Huffman Tree which can then be read off to find the code to use. First the frequency counts for each character used in the data set is calculated, as described above. The two lowest ranked (i.e. lowest counts) characters are 'paired,' forming a 'node' of a tree, where the new node has a count which is the sum of the two characters, and it has 'branches' to each of the two paired characters. These characters will no longer be considered in subsequent pairings. If more than one choice is available when pairing, then it is totally arbitrary which choice is made. The next two lowest values are paired in the same way, but any new nodes formed, with there summed counts, must be considered as if they were characters. This procedure continues until only one node exists at the top of a tree which should have a count total equal to the number of characters in the data set being considered. The 'leaves' of the tree should be the characters that appear in the data set. Codes can now be assigned as follows: starting from the top of the tree, to get to a character one must move down a branch, left or right, to reach a given character. We can assign (arbitrarily) 0 to mean left and 1 to mean right (though the reverse works just as well). So the path from the top of the tree to the leaf containing the character maps out a sequence of 0s and 1s for the left or right transversals. These are the bits which make up the code for that character. All the other characters are assigned codes in the same manner. Let's have an example. Suppose that we wish to encode the short message RINGADINGDING. The frequency table for this example is as follows:
The sequence of lowest frequency pairings is shown in Figure 2.1, below. The final tree now gives us the coding for the characters. Choosing a left branch as 0, and a right branch as 1, we have the codes of R=0000, A=0001, D=001, G=01, I=10 and N=11. As you should be able to see, the most frequent characters have been assigned the shortest codes, and the shorter codes are not prefixes of the longer ones. The message (RINGADINGDING) is thus encodes as:
00001011010001001101101001101101 This is 32 bits which gives a compression ratio (assuming 8 bit ASCII characters in the original message) 48/32 = 1.5:1 (not bad). However, if we received the above encoded message how would we know what the codes were and how they had been assigned. Unfortunately, in our simple scheme, we would also have to pass over the code table in order for the message to be decoded. In our example, this would be an enormous overhead. As data sets get bigger the overhead diminishes and it becomes more practical a method.
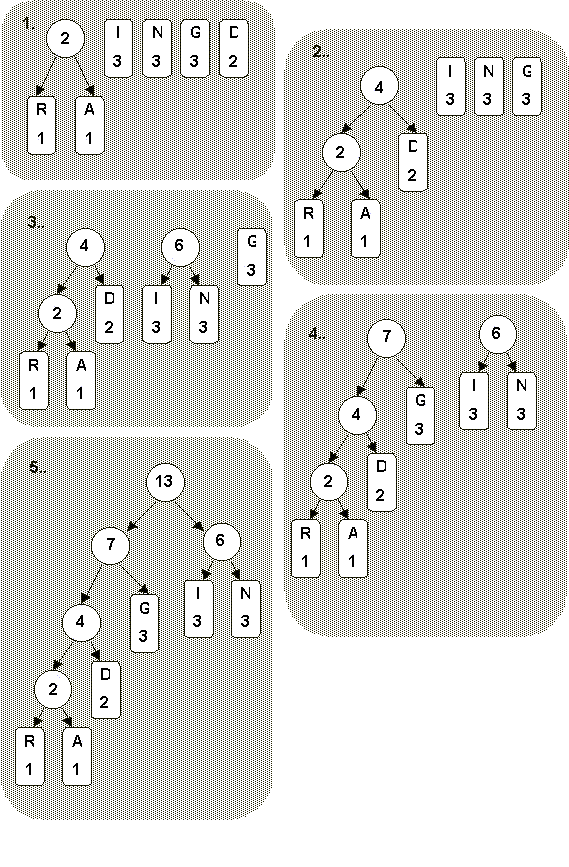
Figure 2.1 Building a Huffman Tree It might be possible to agree a fixed coding table, so that both sender and receiver knew the code mappings and a table needn't be sent. This is fine if the same message is always sent, but every new message will have a different frequency table, and thus a different Huffman tree with its code assignments. Data of similar origin might have similar frequency distributions, for example English text. So we might have an English text code mapping, and could use this if all messages are in English. The compression rate will only be as good as the table, and so care would need to be taken when constructing this 'model.' Many examples of English would need to be used, and unless the message has exactly the frequency distribution of the fixed table we are using, the compression ratio will always fall short of the ideal. This is why you are unlikely to come across this kind of pre-calculated table in any implementation. Constructing and sending the codes for the particular method is more likely, and the penalty in speed efficiency of reading the data twice (once for the mapping, once for the encoding) is bourne. An alternative is to start with all characters being equal probability. As new characters are encoded, the frequency distribution is updated 'on the fly.' As the character ranks change, so do the code assignments. The receiver has the same algorithm available to it. As it decodes data it too keeps relative ranking tracked and adjusts the code mappings in exactly the same manner as the encoder. This has the advantage of obviating the need to transmit the coding table, and the encoded data is not read twice in order to construct the codes. This will still not be as efficient (compression ratio wise) as the Huffman tree construction mentioned above, but is an improvement on fixed tables, with the speed advantages mention, and it is used widely with Huffman and other variable-length coding schemes. 2.3 Arithmetic CodingHuffman coding, mentioned in the previous section, has been described as 'best,' assuming the two pass encoding described above. This is true only if we use codes that are an integer number of bits, and are fixed. A related method is Arithmetic coding (Witten et. al. 1987). With this method codes can be stored in fractions of a bit. The method will achieve at least as good a result as Huffman coding, but will often beat it. The penalty for this gain, as with so many things in engineering, is increased complexity. The basis for the algorithm is to find a unique fractional number for the message being encoded, based on the probability of the symbols appearing in the exact order as in the message. It won't be an exact probability measure, as two messages may have exactly the same probability. As with Huffman encoding, each symbol has a probability of appearing in the message, which is the frequency of the symbol divided by the length of the message. So, for example, if the symbol '#' appears 5 times in a 20 symbol message, its probability is 5/20 = 0.25. For a message to be encoded, all its symbols have their probability calculated in such a manner, with the totals, hopefully, adding to 1 (i.e. there is a 100% chance of finding a symbol that is somewhere in the message). Next, the probability space is divided up into ranges matching the symbol probabilities, stacked on top of each other, as it were. E.g. If a message has a 3 symbol alphabet (A1, A2 and A3, say), and the probabilities for the symbols is 0.25, 0.45 and 0.30, then we would divide the range of 0 to 1 into 0 to 0.25, 0.25 to 0.7 and 0.7 to 1.0. When the first symbol arrives for encoding, we select the range correspondingly (so if it were A2, the the range is 0.25 to 0.7). This new range is now our working range and is divided in to the same proportional segments as was the 0 to 1.0 range initially. When the next symbol is encoded we modify the current range to be the subrange of the first symbols range. So, if the next symbols is A1, then we need the range 0 to 0.25 of the range 0.25 to 0.7, which is 0.25 to 0.3625. This continues for the entire message. The range get narrower, and the decimal fractions get longer. When the entire message is encoded, we can pick on of the range bounds as the encoded message (usually the lower bound). Let's have a more extended example to illustrate these ideas. We wish to encode the message RINTINTIN.(10 characters, including the full-stop.) Firstly we work out the symbol probabilities (which I have made easier by choosing a 10 symbol message.)
Also shown in the table are the range allocations for the symbols, with the upper an lower bound difference equalling the symbols' probabilities. It should be noted that it is arbitrary the order in which the symbols probabilities are allocated, though, of course, the encoder and decoder must agree on this point. So, to start encoding the message, we take the first symbol 'R', and modify the current range to be 0.9 to 1.0. The final encoding will have a value which must lie between (or possibly on) these two values. The next symbol is 'I', with a range of 0.6 to 0.9. We then calculate what this range is within the previously calculated range. So, 0.6 of the way between 0.9 and 1.0 is (0.9 + ((1.0 - 0.9) * 0.6) = 0.96. Similarly, 0.9 of the way between 0.9 and 1.0 is 0.99. So we now know the message values lies between 0.96 and 0.99. We have narrowed the range of possible numbers for our message. This procedure is carried through for the rest of the message's symbols, with the range becoming more and more restricted. The table below shows the results for the entire example message.
As can be seen, the resulting numbers converge toward a particular point, with the difference between the upper and lower bounds becoming smaller and smaller. The final lower bound (0.9711805560) can now be used to uniquely identify the message. To decode the message, the reverse is applied. Since 0.9711805560 lies between 0.9 and 1.0 we know that the first symbol must be 'R'. If we now remove the lower bound values from this number (i.e. 0.9), and divide by the probability for 'R' (0.1), (that is, ((0.9711805560 - 0.9)/0.1), then we get the value 0.71181. Since this lies between 0.6 and 0.9, then the next symbol must be 'I'. This process is repeated to decode the entire message. Now you are probably thinking that not only is this method more complicated than Huffman encoding, but it is very much more complicated than Huffman coding, and is the effort worth it? We have used multiplication and division, with large decimal fractions with many significant figures. Can we even handle this in a computer program or an ASIC? We can, fortunately, and using only integer arithmetic and minimal storage of bits. Firstly, any decimal fraction can be represented as a binary fraction, as one might expect, and, like floating point numbers, decimal places may be inferred, effectively scaling the numbers to be integers. Also, from the table may be noticed that, one a significant figure is the same in both the upper and lower bound values, then it will remain at this value for the rest of he encoding. This means that, when this occurs, we can output that value (or bit), rescale the remaining bits, and continue. With all this it is possible to get sufficient resolution with just 16 bit arithmetic . There is one problem where the value may be converging to a point where (equivalently in decimal) the lower bound values are ...9999... and the upper bound values are ...0000... . This can be solved by 'borrowing' in a similar fashion in arithmetic subtraction. It is mathematically provable (though not by me) that 1.0 = 0.999999... recuring. We can substitute the zeros with this, so long as we remember, and correct the situation once the convergence has resolved one way or the other (i.e. on the ...9999... side or the ...0000... side). So, we can solve some of the practical difficulties, and make this a viable algorithm for use in software or hardware systems. Having said this, the implementation is still not as simple as other alternatives, and this may be why Arithmetic Coding hasn't caught on as one might expect. That isn't to say it hasn't been used. IBM introduced and Arithmetic codec (coder/decoder) implementing a variant called IRDC (Increased Data Recording Capacity-it was used in a tape storage device), which Exabyte, for one, have used. 2.4 ModelsThe Huffman and Arithmetic Coding techniques outlined above both require a table of symbol probabilities-a 'Model.' This can be a 100% accurate model, as used in the examples for these methods, but which requires a time consuming first pass over the data in order to construct the mode, which also needs to be transmitted (or stored) with the data in order to reconstruct the message. Adaptive methods were eluded to in the Huffman discussion. These have the advantage of needing no first pass of the data, and the model may be reconstructed on decoding, obviating the need for transmission or storage of that model with the message. The price paid is decreased compression ratios. Models, ideally, should accurately reflect the probability distribution of the symbol occurences, which, if compression is to occur should be non-uniform. In the above discussions, it has been assumed that a symbol's probability is fixed. This was calculated based on the occurences of the symbols divided by the message length. This takes no account of any other symbol in the message. This is a zero-order model. A symbol's probability does, in fact, jump around quite a bit. For example, a text file may have a space character after every word, which might be a probability of 1 in 10, or 0.1. If the current character is a full-stop, then the probability for a space might rise to 0.7, say. By looking at the context of the character, i.e. the symbols occuring around it, a better statistical model may be obtained. The order of the model indicates the number of symbols used in determining the current symbol's context. So a 2nd- order model will use the two previous symbols in order to calculate the current symbols probability. However, as the model order goes up, so does the memory requirements in order to store statistics for each context. In a zero-order model, with 8 bit symbols, only 256 statistics need to be kept. A 1st order model needs 65536 and a 2nd order model needs 16Mwords. I.e. it quickly gets very silly, and managing the resource also becomes cumbersome, having to search through larger amounts of data, and updating (in adaptive methods) greater table sizes. There is another way; the LZ adaptive coding class of algorithms which we shall look at next. 2.5 LZ Adaptive CodingThe Lempel-Ziv family of compression techniques are what are known as 'substitutional' compression algorithms. They are characterised by the use of 'codewords' to substitute for 'strings' of symbols, which then reference a store to reconstruct the strings on decoding. The methods have some advantages over other methods in that they are 'universal'; i.e. they make no assumption about the data sets symbol probability distributions, and are inherently adaptive. They are also automatically encode the 'model' table within the encoded data, so it can be reconstructed by the decoder, without additional data transmission. There are two main flavours of LZ algorithm LZ1 (also known as LZ77---Ziv et. al. 1977) and LZ2 (also known as LZ78---Ziv et. al. 1978). The first of these is conceptually the simplest to understand, but can be slightly more complicated to implement in software, or indeed hardware). In brief, the last n symbols are kept in a buffer. As new symbols arrive, they are appended to the current 'string' of symbols. If the string is in the buffer, then the string is maintained, and the buffer updated with the new symbol. Once the string has grown to a point where it is no longer in the buffer, the pre-appended string (that was in the buffer) is substituted for a code which consists of a pointer into the buffer where the string occurs, and a run-length indicating how long the string was. The symbol that caused the search to fail now becomes the single symbol string, it is appended to the buffer, and the process continues. Since only the last n symbols are remembered, the buffer can be thought of as a window on the data, n symbols wide, sliding along the data set. Hence you will often find this method called the Sliding Window technique. The buffer is a history of the last n symbols, and so is often referred to as a History Buffer. In its purest form all strings are encoded as pointer/run-length codes, but this is inefficient if the string is a single symbol. Variants might allow single characters to be encoded as 'literals', but then the pointer/run-length codes must be distinguishable from literals. So this is quite a simple method. The difficulty is in determining whether a particular string is in the history buffer, and ensuring the search is exhaustive. This method is, in my experience, easier to do well in hardware than in software, where Context Addressable Memory can be implemented, if not easily, at least with some confidence. More on this later. The second method (LZ2) is similar to LZ1 in its substitutional nature, but uses a 'dictionary' of strings which have previously been seen in the input data, with codewords making references into the dictionary's list of strings, or 'entries.' These codewords are then substituted in place of the strings of symbols. Initially the dictionary contains only the single symbol strings (e.g. values 0 to 255 for 8 bit bytes). As symbols arrive, they are appended to the current string, and the dictionary is searched to see whether it has an entry for that string. If it does, then a new symbol is appended to the current string. This continues until no entry is found in the dictionary for the current string. When this happens a new entry is assigned a codeword, and the string placed in the dictionary entry for that codeword. The codeword for the last matching string is output, and in the purest LZ2 form, the symbol causing the mismatch is also output. However, in the most popular variant, due to Welch (Welch 1984), called LZW, the offending symbol becomes the current single symbol string, and the process continues. So this rounds up four major algorithms (excluding run-length encoding, rarely used on its own), used in varying degrees in both software and hardware implementations. Next I want to look in more detail at one of the more popular LZ algorithms and look at LZW, as a case study, and at what it takes to make it a fully specified and operational algorithm which can be implemented as a hardware codec (usually) as a standard for tape storage devices. 3 The Lempel-Ziv-Welch Compression AlgorithmAs has been mentioned in section 2.5 above, the LZ2 algorithm, in particular the LZW variant, has a dictionary with a number of entries. Each entry has a codeword associated with it, with a unique value. Each entry refers to a string of symbols that have either been seen in the incoming data stream before, or are the single symbol strings that the dictionary was initialised with. From now on, symbols will be 8 bit bytes, with values 0 to 255. It doesn't matter if these bytes represent ASCII codes, or object data or whatever. The entries, with their associated codewords, which represent the single byte strings are known as root entries (or codewords). To make this algorithm practical we will have to start imposing some restrictions on what is allowed. For example, we cannot keep building new entries in our dictionary indefinitely, and it is usual (though not universal) to restrict codewords to be 12 bits wide, giving a possible 4096 codewords, 256 of which must be the root codewords. The other remain unassigned at the start of a compression procedure, and we are free to assign them to particular strings as we choose. In our previous discussions, no limit has been placed on the size of the strings that the dictionary may refer to. There are two reasons why we might want to restrict this. The first is to do with the fact that our dictionary will be held in memory, and we cannot allow the dictionary to grow unpredictably large. Secondly, for reasons that we will come on to, on decompression, we will have to hold entire strings together before outputting the bytes that make them up, and we will want to limit the holding store used to do this. These are practical restrictions, rather than algorithm necessities, but realising the algorithm in tangible form is what we're aiming to do. Now, as each string in a dictionary is one that we have seen in the input data stream, and we only add new entries when we see a string which has not been seen before, but we do always add it, then it must always be the case that a new entry consists of a string that already has an entry in the dictionary, plus a single byte which caused the string to be 'new.' Therefore, we can always make a new dictionary entry by storing a byte value and a pointer to another entry in the dictionary, where the entry pointed to, appended with the byte value equals the new string being added. If a codeword is 12 bits, and the byte takes 8 bits, all 4096 entries in the dictionary will need 80K bits in total. This, then, gives us a predictable maximum dictionary size, which is a manageable quantity. Now I've gone through some of the practical aspects of implementing this algorithm before embarking on describing the actual algorithm in detail, because the algorithm is not independent of practical considerations. It was designed to be implemented in digital form, and the way it is described is based on these practical concerns. So the next section describes the algorithm in more general terms, but you should see that the method is shaped by the restrictions we have placed on our implementation. We will first look at compression, working through an example to illustrate what the process is. The example we will use is of encoding the message RINGADINGDING. 3.1 CompressionThe table below (Table 3.1) shows the sequence of operations when compression the example. It is assumed that, at the start of the compression, the dictionary is in its initial state; i.e. it contains entries for the 256 single byte strings only. So as to avoid getting confused with actual numbers, the following convention will be used. All of the bytes will be represented by their ASCII character (e.g. R). A codeword for a string will have its string surrounded with parentheses; e.g. (IN) is the codeword for the string 'IN'. At this point it won't matter what value is assigned to the codewords, so long as it is understood that they will all be different.
Table 3.1 Compression of RINGADINGDING From the table, the first character input is 'R', as shown in the leftmost column. Since this is the first input of any kind, the current string we are working with must be an empty (or NULL) string. Adding the 'R' now makes it a single character string, as shown in the next column. Is this string in the dictionary? Well, yes. All single character strings are always in the dictionary; that is how it is initialised. The third column indicates this with a tick. When a match is found in the dictionary, no new entry is built (the matched entry already exists), and nothing is output (under normal circumstances). The next character is input, 'I', and the current working string becomes "RI". This string is not in the dictionary. We haven't built any new entries yet, so only single character strings can match. The cross in the third column shows that no match is to be found. So, a new string has been seen, and an entry must be built for it. From an algorithm point of view, the entire string could be stored in any manner, so long as it can be matched against (however inefficiently) at some future point. However, we're working toward a practical implementation, and by introducing a representation, that isn't strictly necessary, now, will save us a lot of trouble later. Since the entry to be built is for a string which must be composed of a string already in the dictionary, plus one character, then all that is needed to store the new string is the codeword for the string already in the dictionary, and the character which, when appended, makes the new string. If it is not clear to you why this works, remember, we keep pulling in characters from the input, appending them to the current string, until the current string is not in the dictionary. Therefore, the current string at that point must be one character longer than a string with a dictionary entry. Thus, shown in column 4 of the table, the new entry is shown as '(R)I', meaning the codeword for the string "R" (a single character string in this case), followed by the character 'I', representing the string "RI". At this point output is required. On a mismatch we output the codeword for the string last matched against. This is the same codeword as was added in the new entry we built (in this case (R) ). Now, you might ask, why not output the codeword for the new entry we just built, as this represents all the input we have had so far? Well, when we decompress the data, we'd be in the unfortunate position of receiving a codeword for a string which wasn't in the dictionary. For example, (RI) would be the first codeword for decompression which clearly cannot exist in a dictionary which is initialised only for single character strings. As we shall see later, even if we don't output new entry codewords as we build them, this problem is not entirely avoided. More of this later. So (R) is output, which still leaves the input character 'I' unrepresented, and so this becomes our new string, lest we forget about it. The next input character is 'N', making a new current string of IN. There is no match in the dictionary, and so '(I)N' is added, as for '(R)I' previously. The codeword '(I)' is output, and the new string becomes "N". Now this procedure remains the same for the next four input characters (G, A, D, I) where four new entries are built ((N)G, (G)A, (A)D and (D)I) and four codewords are output ((N), (G), (A), (D)). Then, something more interesting happens (at last!). We have "I" as our unprocessed string, and 'N' as our input character, giving us "IN", which is (hurrah!) in the dictionary, built at row 3. Now all we have to do is remember the entry for "IN" (stored as (I)N) and input the next character. No codeword is output, and no new entry is built. The next character input is 'G', giving us "ING" as our current string, and this is not in the dictionary. In fact, no three character entries have yet been built. The procedure for a failed match applies once more. A new entry is built, stored as (IN)G. That is, the entry number for (IN) is stored, along with the character value for 'G'. The string we have matched is output (i.e. (IN)); the first dynamically generated entry codeword. And the current string is set to "G". The rest of the input is processed in the same manner, until the end. There is one further match to a dynamically generated dictionary entry, and it is processed in the same manner as described above. The only thing left to clear up is what to do with the end of the data stream. It will always be the case that at the end of processing there will be a string that is matched in the dictionary, but has not been represented in the output. This could be a single character string, or, as in our example a match with a dynamically allocated entry. Since the normal procedure is to carry it forward for appending the next input character, we must do something different, since no more input is forthcoming. In this case we simply 'pretend' that there is no match, and output the codeword for the current outstanding string. No entry is built, and the current string is effectively set to the null string. All the input has been represented in the output, in an encoded form, which must, therefore, contain enough information about the original data to recover it. It doesn't explicitly contain the dictionary, but, as we shall soon see, this too has been encoded in the output data; a feature which is one of the major attractions to this class of algorithm. So, without further ado, let's decompress the encoded data, and see what happens. 3.2 DecompressionIn decompression, the input must consist of the codewords we have previously generated as the compressed output, in the order in which we generated them. These will be, as in our compression example, a mixture of root codewords and dynamically allocated codewords. We can only start with an initialised dictionary, as the final compression dictionary has not been stored with the data. This restricts the point at which decompression can begin within a compressed data set. Only at points where the dictionary was in its initial state during compression can decompression begin. In the simple examples here, this means at the beginning of the data. Table 3.2 below shows the decompression sequence for our previously compressed example. The first six codewords are all root codewords, and their byte values may be sent directly to the output. At each stage (except for the first codeword) a dictionary entry is built with a byte value of the current input codeword, and a pointer to the previously processed codeword's dictionary entry. I.e. an entry representing the last string processed with the current codeword's byte value appended to it. Hence the first entry built is (R)I, since, when (I) is input, the last codewords processed was (R) and the byte value of (I) is 'I'.
Table 3.2 Decompression of Previously Compressed Data
The seventh codeword input is (IN); a non-root codeword. It already has an entry in the dictionary at this point, as show on the third line in the figure. This entry has a byte value of 'N', and so this is placed on a 'LIFO'. LIFO stands for 'last in first out'. As we follow this example through, you will see that the byte values recovered in a multi-byte codeword are in reverse order. Therefore we must store them until the entire string is decoded, and then output them in the correct order. A 'LIFO' is used, where we can 'push' bytes into it, and then 'pop' them when we have all the bytes-the last byte pushed being the first byte popped. The entry for (IN) also has a pointer to another entry; in this case it is the root entry (I). Its byte value is also pushed onto the LIFO and, as it is a root codeword, the contents of the LIFO flushed to the output. At this time, an entry is built using the same rules as before. The new entry has a pointer to the previously processed codeword (i.e. (D)) and a byte value equal to the current codeword's. Since we terminated the link list traversal pointing to (I), the byte value is 'I', as shown in the figure. The rest of the input codewords are processed in a similar manner, with the entire original data recovered, and the dictionary left in the same state as at the end of compression. So, we have managed to recover the data, without loss of information, and without storing the dictionary---all was encoded uniquely within the compressed data itself. And that would be all there is to it, except there is one slight twist in the tale. There is a circumstance where, during decompression, a codeword is encountered which has no entry in the dictionary! This is the KωK exception case. 3.3 The KωK Exception CaseWelch describes in his paper a particular corner case in the LZW algorithm which, if processed as described above, will cause a breakdown of the procedure. It is called the KωK (kay-omega-kay) exception case, since inputting the sequence KωK, where K is any single character and ω is a string for which there is a dictionary entry, causes a codeword for the string KωK to be output (during compression) at the same time as it is built in the dictionary. This causes a problem on decompression since no entry will have been built on encountering it, as entries are built after the codeword is processed. More properly, the sequence KωKωK causes the problem, and the clue to its solution is in the fact that the entry needed is the very next entry we would have built at the end of processing the codeword causing the problem. So, we might have enough information to construct the missing entry uniquely, and recover the situation. To see how, an example is in order. The simplest KωK sequence is the repeated character. This is because K can be any character, and all single character strings have entries in the dictionary be default. Table 3.3 below shows a repeated character compression sequence.
Table 3.3 Repeated Character Compression Case The procedure followed is, I hope you can see, exactly that in the previous compression example. Entries are built when no match is found, and the last character input is carried forward as the new current string. Now, if we are presented with the codeword sequence shown in the output column of the figure, what will happen? We can process the first codeword as it is a root codeword with a know byte value. No entry can be built, as no previous codeword has been processed. The next codeword is (KK). But this is a dynamically allocated codeword, and we haven't built any entries yet. There are a couple of slightly different methods for detecting, and then correcting this problem, but, basically, the problem is detected if the value of the codeword is the same as the next dictionary entry that will be built (and they are built in ascending order). It is corrected by placing the byte value of the last processed codeword onto the LIFO, and re-submitting the last codeword value again in place of the current problematic one. This will, once the FIFO is flushed, place the right characters on the output, and will result in the 'missing' dictionary entry being built, using the normal procedures. An alternative exists where the missing entry is built first, but the result is just the same, and it is left to the reader to figure out the details. This final detection and correction works for all KωK cases, and ties up the last lose end, as far as the basic algorithm goes. Describing an algorithm and manipulating symbols on paper shows how an algorithm might work, but we haven't arrived yet at a method which is fully practical. There are still some details to consider before the above can become a working piece of software, or a digital hardware implementation. Some additional (fortunately much simpler) algorithms need to be roped in, and some design constraints and limits placed on the algorithm to map the symbolic representation onto more practical units of information, such a bytes. But that must wait for the next article. Last updated 16th July 2007 © 1999-2007 Simon Southwell. All rights reserved. simon@anita-simulators.org.uk | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
